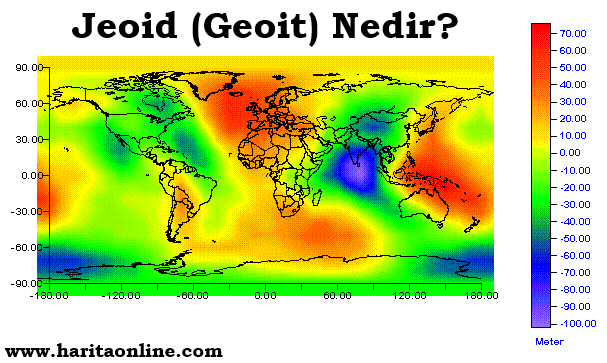
Yükseklik yeryüzündeki geometrik cisimlerin üçüncü boyutudur. Bir noktanın yüksekliği, noktadan sıfır yükseltili başlangıç yüzeyine inilen dikin boyudur. Noktanın yüksekliğini saptayabilmek için ilk olarak başlangıç yüzeyinin tanımlanması ve buna dik doğruların belirlenmesi gerekir. Yeryüzü noktaları için en kolay belirlenebilen doğrultular çekül doğrultularıdır. Bunun için yükseklik belirlemede bu doğrultuların alınması en kolay yoldur. Bu doğrultulara dik sıfır yükseltili yüzey ise jeoid yüzeyidir. Jeoidin belirlenmesi de jeodezinin temel görevlerinden birisidir (Ayan,1978).
1970’li yıllardan başlayarak günümüze kadar hızlı bir gelişme gösteren GPS, jeodezik çalışmalarda çok uzun zamandan beri kullanılmakta olan klasik ölçme yöntemlerinden kaynaklanan problemlerin aşılmasında oldukça önemli rol oynamıştır. Bugün ulaştığı teknik imkânlarla GPS alıcısına sahip olan her kullanıcı gerektiğinde hassas bir şekilde, üç boyutlu olarak konum bilgilerini elde edebilmektedir.Yöntemin temel ilkesi, uzayda değişik yörüngelerde bulunan en az 4 uyduya mesafe ölçümü yaparak alıcının üç boyutlu koordinatlarının hesaplanmasıdır. Burada uydular, koordinatları bilinen noktalar olarak kabul edilirse, işlem en basit anlamda bir uzay geriden kestirme yöntemidir.
Uydu ile alıcı arasındaki uzaklık (jij), uydu koordinatları (xj, yj, zj), alıcı koordinatları (Xi, Yi, Zi) olarak alındığında;
şeklindedir. GPS verilerinin değerlendirilmesi ile elde edilen yükseklikler elipsoidal yüksekliklerdir. Bunun yanında genellikle pratik uygulamalarda elipsoidal yükseklik kullanılmaz, bunun yerine ortometrik yükseklik kullanılır. Bu yüzden GPS ile elde edilen elipsoidal yükseklikler ile ortometrik yükseklikler arasında ilişki kurulmalıdır. GPS ile koordinatlandırılmış üç boyutlu konum ağları geometrik bir sistem olmasına karşılık mevcut yükseklik ağları düşey boyutun jeopotansiyel ile ifade edildiği tek bileşenli fiziksel bir sistemdir. İki sistemi ilişkilendirmekteki asıl amaç, GPS ölçülerine göre daha yorucu olan ve zaman alan nivelman işlemini azaltarak GPS ile sorunu çözmektir. Bunun için dm’nin altında bir doğrulukla jeoidin belirlenmesi gerekir (Aksoy vd.,1998). Jeoid belirlenmiş ise elipsoidal yükseklik ( h ) ile ortometrik yükseklik ( H ) arasındaki ilişki,
H = h – N
şeklindedir. Bu eşitlikte N jeoid yüksekliğidir. GPS verilerinden yararlanarak yükseklik belirlemenin temelini veren bu eşitlik ile, N değeri bilinen ve h değeri GPS gözlemleriyle saptanmış olan noktanın ortometrik yüksekliği hesaplanabilir. Hesaplanacak ortometrik yüksekliğin doğruluğu, N değerinin ve GPS ile elde edilen elipsoidal yüksekliğin doğruluğuna bağlı olarak değişir.
JEOİD YÜKSEKLİĞİ BELİRLENMESİNDE KULLANILAN MATEMATİKSEL MODELLER
Jeoid ile elipsoid yüzeyi arasındaki uzaklığa jeoid ondülasyonu veya jeoid yüksekliği adı verilir. Yeryüzünü oluşturan tabakaların yoğunluklarının farklı olmasından dolayı jeoid düzensiz bir şekle sahiptir. Jeoid yüksekliği değerleri ortalama yer elipsoidine göre ± 100 m arasında değişir.
JEOİD YÜKSEKLİĞİ BELİRLENMESİNDE KULLANILAN MATEMATİKSEL MODELLER
Jeoid ile elipsoid yüzeyi arasındaki uzaklığa jeoid ondülasyonu veya jeoid yüksekliği adı verilir. Yeryüzünü oluşturan tabakaların yoğunluklarının farklı olmasından dolayı jeoid düzensiz bir şekle sahiptir. Jeoid yüksekliği değerleri ortalama yer elipsoidine göre ± 100 m arasında değişir.
Jeoid belirleme yöntemlerini jeoidin kapsadığı alana göre ve kullanılan verilere göre iki grupta incelemek mümkündür: Jeoidin kapsadığı alana göre global, bölgesel ve yerel jeoid belirleme söz konusudur. İkinci grupta yer alan veriler çekül sapmaları, nokta gravite ölçüleri, GPS/Nivelman, GPS/Astronomik gözlemleri ve uydu ile yersel verilerin kombinasyonudur.
1) Global Jeoid Belirleme Modelleri
Global jeoid modelleri, isminden de anlaşıldığı üzere tüm dünyaya ait gravite bilgilerinden faydalanarak oluşturulmuş bir modeldir. Her ulusun bir ya da birkaç istasyonu dünya çapındaki gravite baz istasyonları ağını. IGSN71 datumu, 1906’da yapılan sarkaç ölçüleri ile belirlenen Potsdam sisteminin yerini almış ve gravite ölçüleri için referans olarak kabul edilmiştir.
1) Global Jeoid Belirleme Modelleri
Global jeoid modelleri, isminden de anlaşıldığı üzere tüm dünyaya ait gravite bilgilerinden faydalanarak oluşturulmuş bir modeldir. Her ulusun bir ya da birkaç istasyonu dünya çapındaki gravite baz istasyonları ağını. IGSN71 datumu, 1906’da yapılan sarkaç ölçüleri ile belirlenen Potsdam sisteminin yerini almış ve gravite ölçüleri için referans olarak kabul edilmiştir.
R :
G :
Dg :
S (y ) : Stokes fonksiyonu
Stokes formülü , jeoidin dış tarafında kitle olmadığı ön kabulüne dayanır. Eğer herhangi bir fiziksel jeodezi problemi, potansiyel kuramının belirlediği anlamda bir sınır değeri problemi olarak ele alınmak istenirse, sınırlayan yüzeyin dışında kitle yoktur diyen bu kabul zorunludur. Bunun nedeni, potansiyel kuramının sınır değeri problemlerinin daima harmonik fonksiyonları içermesidir. Jeoidin dış tarafında kitleler varolduğundan Stokes integrali ya da ilgili formüllerin uygulanabilmesinden önce bu kitlelerin jeoidin içine götürülmesi ya da tümüyle ortadan kaldırılması zorunludur. Türlü gravite indirgemelerinin amacı budur.
Global jeoid modellerine örnek olarak potansiyel katsayılardan yararlanarak jeoid yüksekliği hesaplama ilkesine dayanan OSU91-A ve EGM 96 modelleri verilebilir.
OSU91-A ( Ohio State University Global Jeoid Model 91 A ) Modeli
1.1. Bölgesel Jeoid Belirleme Modelleri
Bölgesel jeoid modellerinin gravimetrik olarak hesaplanması işlemi Stokes integraline dayanır:
Gravimetrik yöntemler, bir sınır yüzey için verilen gravite anomalileriyle bu yüzeye bağlı jeoid yükseklikleri ya da yükseklik anomalileri arasındaki ilişkiyi tanımlayan jeodezik sınır değer probleminin çözümü temeline dayanır. Sınır değer probleminin çözümü Stokes entegrali ile sağlanır. Stokes entegrali,
- klasik
- hızlı Fourier
- vb. tekniklerle çözülebilir.
2.1. Klasik ve Hızlı Fourier Tekniği ile Stokes İntegrasyonu
Jeoid yüksekliğinin hassas bir şekilde belirlenebilmesi için; jeopotansiyel model (GM), ortalama serbest hava gravite anomalileri (DgFA)
2.1. Klasik ve Hızlı Fourier Tekniği ile Stokes İntegrasyonu
Jeoid yüksekliğinin hassas bir şekilde belirlenebilmesi için; jeopotansiyel model (GM), ortalama serbest hava gravite anomalileri (DgFA)
N = NGM + NDg + Nh
Dg =
DgFA - DgGM - Dgh
Düzlem yaklaşımda E bir integrasyon alanı ve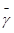 ortalama gravite olmak üzere jeoid yükseklikleri aşağıdaki eşitlik ile hesaplanır:
ortalama gravite olmak üzere jeoid yükseklikleri aşağıdaki eşitlik ile hesaplanır:
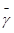 ortalama gravite olmak üzere jeoid yükseklikleri aşağıdaki eşitlik ile hesaplanır:
ortalama gravite olmak üzere jeoid yükseklikleri aşağıdaki eşitlik ile hesaplanır:
Yukarıdaki eşitlikte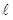 değeri, data noktaları (x,y) ile hesaplanan noktalar (xp, yp)
değeri, data noktaları (x,y) ile hesaplanan noktalar (xp, yp)
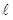 değeri, data noktaları (x,y) ile hesaplanan noktalar (xp, yp)
değeri, data noktaları (x,y) ile hesaplanan noktalar (xp, yp)
eşitliği kullanılarak hesaplanır. R ortalama Dünya yarıçapını, S(y) Stokes fonksiyonunu, y
2.2. En Küçük Karelerle Kolokasyon Yöntemi
2.2. En Küçük Karelerle Kolokasyon Yöntemi
N = N1 + N2 +N3
N1 :
N2 :
N3 :
Benzer olarak jeoid yükseklikleri farkları ;
DN = DN1+DN2+DN3
şeklinde yazılabilir.
Jeoid yüksekliğine ait uzun dalga boylu sinyaller (N1) belirli bir dereceye kadar olan katsayıların oluşturduğu jeopotansiyel modelin sonlu küresel harmoniklerde kullanımı ile elde edilebilir (lmax).
Jeoid yüksekliğine ait uzun dalga boylu sinyaller (N1) belirli bir dereceye kadar olan katsayıların oluşturduğu jeopotansiyel modelin sonlu küresel harmoniklerde kullanımı ile elde edilebilir (lmax).
Bu eşitlikte ;
GM :
g :
DC, DS :
q, l :
Plm (.) :
a :
r :
anlamındadır.2.3. Kolokasyon ve İntegrasyon Metodlarının Kombinasyonu Modeli
Bu metodda s= CSX Cxx-1x eşitliğinden hesaplanan nokta etrafındaki küçük bölgede NDg’nin
Burada:
S(y) :
y :
a : y’nin
R: Dünya’nın ortalama yarıçapıdır.
3) Astrojeodezik Yöntem İle Jeoid Yüksekliği Belirleme
Fiziksel yeryüzündeki bir P noktasından geçen çekül eğrisi ile yine aynı noktadan geçen elipsoid normali e kadar birbirlerinden saparlar. Bu farka çekül sapması denir ve
3) Astrojeodezik Yöntem İle Jeoid Yüksekliği Belirleme
Fiziksel yeryüzündeki bir P noktasından geçen çekül eğrisi ile yine aynı noktadan geçen elipsoid normali e kadar birbirlerinden saparlar. Bu farka çekül sapması denir ve
e = xcosa + hsina
eşitliği ile ifade edilir.
a :
x , h :
Astrojeodezik jeoid belirleme yönteminde çekül sapması bileşenleri, aynı noktaya ait jeodezik ve astronomik koordinatların karşılaştırılması ile elde edilir. Bu işlemde j, l jeodezik enlem ve boylam; f, L
x= f - j
h= (L-l)
cosj
Başlangıç noktası A’da jeoid yüksekliği biliniyor ise (NA)
eşitliğiyle hesaplanır.
4) GPS/NİVELMAN Yöntemiyle Elde Edilen Verilerden Yararlanarak, Analitik Bir Yüzey Geçirerek Geometrik Olarak Jeoid Yüksekliği Belirleme
Elipsoidal yüksekliklerin ve ortometrik yüksekliklerin her ikisinin de bilindiği noktaların mevcut olduğu durumlarda, GPS/NİVELMAN jeoidi belirlenirken yükseklik eğrili haritaların yapımı için bu noktalardan bir yüzey geçirilir. Yüzey geçirilmesiyle elde edilen model, ara noktaların jeoid yüksekliklerinin belirlenmesinde de kullanılır. Ara noktaların elipsoidal yükseklikleri GPS ile bulunur. Modelle ortometrik yükseklik elde edilir. Bu işlem astrojeodezik yönteme benzer. Her iki yöntemde de gözlemden kaynaklanan hatalar dışında en yüksek hassasiyet, jeoidin düzgün olduğu alanda bulunan birbirine 3-5 km istasyonlar arasında yapılan uygulamalarda elde edilir.
4.1. Polinomlar İle Yüzey Oluşturma
4) GPS/NİVELMAN Yöntemiyle Elde Edilen Verilerden Yararlanarak, Analitik Bir Yüzey Geçirerek Geometrik Olarak Jeoid Yüksekliği Belirleme
Elipsoidal yüksekliklerin ve ortometrik yüksekliklerin her ikisinin de bilindiği noktaların mevcut olduğu durumlarda, GPS/NİVELMAN jeoidi belirlenirken yükseklik eğrili haritaların yapımı için bu noktalardan bir yüzey geçirilir. Yüzey geçirilmesiyle elde edilen model, ara noktaların jeoid yüksekliklerinin belirlenmesinde de kullanılır. Ara noktaların elipsoidal yükseklikleri GPS ile bulunur. Modelle ortometrik yükseklik elde edilir. Bu işlem astrojeodezik yönteme benzer. Her iki yöntemde de gözlemden kaynaklanan hatalar dışında en yüksek hassasiyet, jeoidin düzgün olduğu alanda bulunan birbirine 3-5 km istasyonlar arasında yapılan uygulamalarda elde edilir.
4.1. Polinomlar İle Yüzey Oluşturma
eşitliği genel yüzey eşitliğidir. n sayısı 1 ise geçirilen yüzey bi-lineer, 2 ise bi-quadratik ve 3 olduğunda bi-kübik spline adını almaktadır. Bi-lineer yüzeyde ortak nokta sayısı (elipsoit ve ortometrik yüksekliği belli) en az 4, bi-quadratik yüzeyde en az 9 ve bi-kübik spline yüzeyde en az 16 olmalıdır. Ortak nokta sayısının bu değerlerden fazla olması durumunda yüzeyi belirleyen parametreler en küçük kareler yöntemine göre dengeleme ile hesaplanır. Üstteki eşitlikteki ai değeri spline katsayısını, x ve y değerleri sözkonusu noktanın Gauss koordinatlarını ifade eder (İnal, 1996). Polinomun derecesi dayanak nokta sayısına bağlı olarak belirlenir. En yüksek dereceden başlayarak bulunan katsayıların istatik testlerle signifikant olup olmadıkları belirlenerek kesin sonuç bulunur. Derece önceden belirlenemez. Derece; nokta sayısı, doğruluk, jeoidin özelliğine bağlı olarak oluşur.
4.2. İnterpolasyon Yöntemleri
Arazi üzerinde dağılmış, koordinatları (x, y, z) bilinen noktalara “Dayanak Noktaları” adı verilir. Belirtilen arazinin bulunduğu koordinat sisteminin yatay düzleminde düzgün ve yeter sıklıkta bir ağ oluşturulur. Dayanak noktaları bu ağın içinde ve dışında dağılmış durumdadırlar. Daha sonra ağın köşe noktalarının yükseklikleri çeşitli interpolasyon yöntemlerinin herhangi birinden yararlanılarak hesaplanır. Böylelikle arazi sayısal olarak belirlenmiş olur.
4.2. İnterpolasyon Yöntemleri
Arazi üzerinde dağılmış, koordinatları (x, y, z) bilinen noktalara “Dayanak Noktaları” adı verilir. Belirtilen arazinin bulunduğu koordinat sisteminin yatay düzleminde düzgün ve yeter sıklıkta bir ağ oluşturulur. Dayanak noktaları bu ağın içinde ve dışında dağılmış durumdadırlar. Daha sonra ağın köşe noktalarının yükseklikleri çeşitli interpolasyon yöntemlerinin herhangi birinden yararlanılarak hesaplanır. Böylelikle arazi sayısal olarak belirlenmiş olur.
İnterpolasyon n boyutlu Pi noktalarındaki m boyutlu vektörleri kullanarak n boyutlu Pk noktalarındaki m boyutlu bilinmeyen vektörlerinin hesaplanması işlemidir. n boyutlu Pi
noktalarına dayanak uzayı adı verilir. Sayısal arazi modellerinin interpolasyonu probleminde dayanak uzayının iki boyutu (x, y), vektörlerin bir boyutu (z) vardır.
Uygulamada en küçük parçalardaki polinomlarla interpolasyon ve kayan yüzey yardımıyla interpolasyon yöntemleri kullanıldığından yalnızca bu iki interpolasyon yöntemi irdelenecektir.
4.2.1 En Küçük Parçalardaki Polinomlarla İnterpolasyon
noktalarına dayanak uzayı adı verilir. Sayısal arazi modellerinin interpolasyonu probleminde dayanak uzayının iki boyutu (x, y), vektörlerin bir boyutu (z) vardır.
Uygulamada en küçük parçalardaki polinomlarla interpolasyon ve kayan yüzey yardımıyla interpolasyon yöntemleri kullanıldığından yalnızca bu iki interpolasyon yöntemi irdelenecektir.
4.2.1 En Küçük Parçalardaki Polinomlarla İnterpolasyon
Bu yöntemin en genel karakteri, her bir yerel yüzeyin aynı anda hesaplanmasıdır. Dayanak noktaları düzlemi eşit kare veya dikdörtgen parçası üzerindeki yüzeyler tüm bölgede sürekli ve düzgün olacak biçimde düşük dereceden polinomlarla gösterilir.
Eşit kare parçalarındaki yerel polinomlar;
şeklindedir.
Her bir kare bölgesindeki yüzey üstteki eşitlik şeklindeki yüzey fonksiyonu ile gösterilir. Birim karelerin her noktasında yüksekliğe ek olarak y ve x eksenleri doğrultusundaki eğimler de hesaplandığından her bir kare bölgesi için 12 değer bulunmuş olur. Bu değerlerle 12 katsayılı,
Z=a00+a01y+a02y2+a03y3+a10x+a11xy+a12xy2+a13xy3+a20x2+a21x2y+a30x3+a31x3y
şeklinde bikübik bir polinom belirlenebilir. Bu polinom birim karenin köşe noktalarındaki yükseklikler veya eğimlerden hesaplandığından komşu karelerdeki polinomların fonksiyon değerleri sınırlar boyunca aynı olur.
4.2.2. Kayan Yüzey Yardımı İle İnterpolasyon
İstenilen bir noktanın yüksekliği çevresinde bulunan dayanak noktalarından hesaplanan bir yüzeyden elde edilir. Bu yüzeyin konum ve şekli, bir noktadan diğer bir komşu noktaya değiştiğinden “Kayan Yüzey” olarak tanımlanır. Koordinat sisteminin başlangıcı olarak yüksekliği hesaplanacak nokta alınırsa, bu yüzeye ait,
4.2.2. Kayan Yüzey Yardımı İle İnterpolasyon
İstenilen bir noktanın yüksekliği çevresinde bulunan dayanak noktalarından hesaplanan bir yüzeyden elde edilir. Bu yüzeyin konum ve şekli, bir noktadan diğer bir komşu noktaya değiştiğinden “Kayan Yüzey” olarak tanımlanır. Koordinat sisteminin başlangıcı olarak yüksekliği hesaplanacak nokta alınırsa, bu yüzeye ait,
m’nci dereceden polinomun sabit terimi a00
aij, katsayıları, m yüzeyin derecesini göstermektedir. Yüzeyin aij
şeklindedir. Burada xn, yn, n’nci dayanak noktasının koordinatlarını, xo ve yo yüksekliği hesaplanacak olan noktanın koordinatları, Zn
wn = ( (xn – xo)2
+ (yn-yo)2 )-k
eşitliği kullanılır. Burada n indisi dayanak noktalarını, o indisi interpole edilecek noktayı göstermektedir.
Hata denklemleri matris gösterimi ile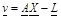 şeklindedir. Burada
şeklindedir. Burada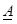 , xn ve yn koordinatlarını içeren katsayılar matrisi
, xn ve yn koordinatlarını içeren katsayılar matrisi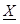 , aij katsayılarını içeren bilinmeyenler vektörü
, aij katsayılarını içeren bilinmeyenler vektörü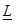 ise, dayanak noktalarının Zn yükseklik değerlerini içeren ölçüler vektörüdür. Buradan,
ise, dayanak noktalarının Zn yükseklik değerlerini içeren ölçüler vektörüdür. Buradan,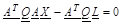 olarak elde edilen normal denklemlerden, aij katsayılarını içeren
olarak elde edilen normal denklemlerden, aij katsayılarını içeren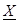 bilinmeyenler vektörü,
bilinmeyenler vektörü,
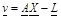 şeklindedir. Burada
şeklindedir. Burada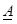 , xn ve yn koordinatlarını içeren katsayılar matrisi
, xn ve yn koordinatlarını içeren katsayılar matrisi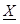 , aij katsayılarını içeren bilinmeyenler vektörü
, aij katsayılarını içeren bilinmeyenler vektörü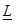 ise, dayanak noktalarının Zn yükseklik değerlerini içeren ölçüler vektörüdür. Buradan,
ise, dayanak noktalarının Zn yükseklik değerlerini içeren ölçüler vektörüdür. Buradan,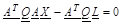 olarak elde edilen normal denklemlerden, aij katsayılarını içeren
olarak elde edilen normal denklemlerden, aij katsayılarını içeren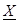 bilinmeyenler vektörü,
bilinmeyenler vektörü,
eşitliği ile hesaplanır.
5) Sonlu Elemanlarla Jeoid Yüksekliği Belirleme
Son yıllarda özellikle Avrupa’da kullanılan, uygulama olanağı oldukça fazla olan bir yöntemdir. Sonlu elemanlar yöntemi; sürekli bir sistemi problemin karakterine uygun sonlu elemanlara ayırarak daha sonra bu elemanların birleştirilmesi tarzında bir uygulama getirir. Jeoid yüksekliği belirlenecek alan parçalara ayrılarak, bu parçalarda interpolasyon yapılır ve komşu parçaları birleştiren düğüm noktalarında süreklilik sağlanır. Sonlu eleman ağının parçalarına ait düğüm noktaları, jeodezik ağın noktalarından farklı olabilir.
5) Sonlu Elemanlarla Jeoid Yüksekliği Belirleme
Son yıllarda özellikle Avrupa’da kullanılan, uygulama olanağı oldukça fazla olan bir yöntemdir. Sonlu elemanlar yöntemi; sürekli bir sistemi problemin karakterine uygun sonlu elemanlara ayırarak daha sonra bu elemanların birleştirilmesi tarzında bir uygulama getirir. Jeoid yüksekliği belirlenecek alan parçalara ayrılarak, bu parçalarda interpolasyon yapılır ve komşu parçaları birleştiren düğüm noktalarında süreklilik sağlanır. Sonlu eleman ağının parçalarına ait düğüm noktaları, jeodezik ağın noktalarından farklı olabilir.














Yorum Gönder
Yorumlama biçimi: Anonim seçerek yorumlarınızı yapabilirsiniz.